Archaeology and Logarithms

Archaeology, as defined by Merriam-Webster, is "the scientific study of material remains (as fossil relics, artifacts, and monuments) of past human life and activities". Within the study of these activities, it is necessary to accurately date discovered artifacts, so that they can be evaluated in the proper way. To do this, archaeologists use the Carbon 14 dating process, to determine the age of the artifact. This type of dating was used to determine the age of Dinosaur fossils, as well as the famous Dead Sea Scrolls.

In this process, archaeologists compare the decaying Carbon-14 in the artifact to the Carbon-12, which remains constant even after death. The half life of Carbon-14 is about 5,730 years.

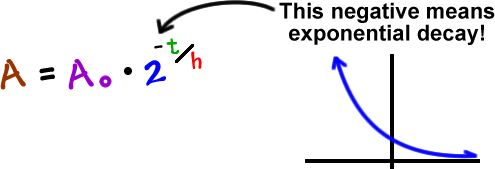
The formula for Carbon-14 decay is

A (final amount)= a(initial amount) x 2 ^time/half life

Example Problem:

In an archaeological dig in Kazakhstan, archaeologists find the teeth of a Tyrannosaur. A live Tyrannosaur was believed to have .05mg of Carbon-14 in its teeth, the teeth that are found have 0.00000579mg. How old are the teeth?

1. First, we must re-write the equation to solve for time.

t= h ln(A)

-----------

ln(1/2)

2. Now, we fill in our data

t= (5730)ln(.0010)

--------------

ln(1/2)

3. Plugging this equation into our calculator, we should get an answer of 99690.57: about 99,691 years old! Since Tyrannosaurus Rex was believed to have gone extinct 65 million years ago, these might not be Tyrannosaur teeth after all!